트리 구조
트리 구조는 정보의 항목들이 가지(branch)로 연결될 수 있도록 하는 자료 구조이다.
트리를 이해하고 구현하려면 아래의 용어들을 이해해야 한다.

우선, A-C 노드의 관계를 보면 A를 부모 노드, C를 자식 노드라 한다. 아래는 나머지 용어를 정리한 것이다.
- 루트 노드(root node): 부모가 없는 노드
- 단말 노드(leaf node): 자식이 없는 노드
- 내부 노드(Internal node): 그 외의 나머지 노드
- 형제(sibling): 같은 부모를 가지는 노드
- 노드의 레벨(level): 루트의 레벨을 l으로 정하였으면, 그 자식의 레벨은 l + 1
- 노드의 깊이(depth) 또는 높이(height): 그 트리가 속한 노드의 최대 레벨
- 노드의 차수(degree): 한 노드의 서브 트리의 수
- 트리의 차수(degree of tree): 트리의 최대 차수
이진 트리
자식 노드가 최대 2개인 트리를 이진 트리라 하며, 모든 일반 트리는 이진 트리로 표현 가능하다.
컴퓨터에서 일반 트리로는 자식 노드가 몇 개인지 예측 불가능 하기 때문에 이진 트리로 표현하는 경우가 많다. 또, 모든 자식 노드가 0 또는 2개인 완전 이진 트리, 리프 노드를 제외한 모든 노드의 자식이 2개인 포화 이진 트리 등으로 나뉜다.
포인터를 이용한 이진 트리의 구현(C++)
template <class T> class Tree; //전방 선언
template <class T>
class TreeNode {
friend class Tree<T>;
private:
T data;
TreeNode* leftChild;
TreeNode* rightChild;
public:
TreeNode(T data=0, TreeNode* leftChild=null, TreeNode* rightChild=null){
this->data = data;
this->left = left;
this->right = right;
}
};
template <class T>
class Tree {
private:
TreeNode<T>* root;
public:
Tree(T data = 0) {
root = new TreeNode<T>(data);
}
//이 외의 트리 연산들(순회 등)
}
map과 unordered_map
map은 트리의 일종인 레드-블랙 트리를 사용한 STL이다.
Pair 형태로 Key와 Value를 가지며 Key는 자동으로 정렬된다.
반면, unordered_map은 비슷하지만 키가 자동으로 정렬되지 않는다.
map을 이용한 이진 트리의 구현
아래의 사진과 같은 트리가 있을 때, map을 이용하여 이진 트리를 구현해본다.
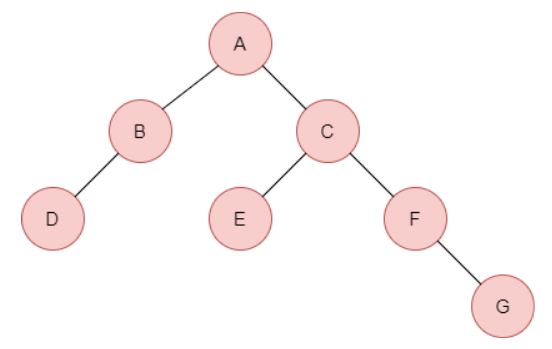
트리의 선언은 아래와 같다.
map<char, pair<char, char> > tree;저장되어 있는 값은 알파벳이기 때문에 character 타입으로 선언하였고 키 값에는 본인이 갖고 있는 알파벳, pair에는 각각 왼쪽 자식, 오른쪽 자식을 갖게 된다.
A는 자식으로 B, C를 갖고 있고
B는 왼쪽 자식에는 D, 오른쪽 자식은 없으며
D는 자식이 없는 리프 노드이다. 이는 아래와 같이 나타낼 수 있다.
tree['A'] = make_pair('B', 'C');
tree['B'] = make_pair('D', '.');
tree['D'] = make_pair('.', '.');값이 없음을 나타내는 규칙은 본인이 정하는 것이다. '.'이 아닌 다른 값으로 나타내도 된다.
모든 값을 할당하였으면 아래와 같이 각 자식에 접근할 수 있다.
tree['A'].first // A의 왼쪽 자식
tree['A'].second // A의 오른쪽 자식
예제
트리의 이해를 돕기 위해 아래의 문제를 풀어본다.
https://www.acmicpc.net/problem/11725
11725번: 트리의 부모 찾기
루트 없는 트리가 주어진다. 이때, 트리의 루트를 1이라고 정했을 때, 각 노드의 부모를 구하는 프로그램을 작성하시오.
www.acmicpc.net
트리의 전위 순회, 중위 순회, 후위 순회를 알아보기 위해 아래의 문제를 풀어본다.
https://www.acmicpc.net/problem/1991
1991번: 트리 순회
첫째 줄에는 이진 트리의 노드의 개수 N(1 ≤ N ≤ 26)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 노드와 그의 왼쪽 자식 노드, 오른쪽 자식 노드가 주어진다. 노드의 이름은 A부터 차례대로 알파
www.acmicpc.net
'Programming Solve > 자료구조 & 알고리즘' 카테고리의 다른 글
| 다익스트라 알고리즘 (0) | 2022.03.17 |
|---|---|
| 이진 탐색(Binary Search) (0) | 2022.03.03 |
| 정렬의 종류 및 구현(C++) (0) | 2022.03.01 |
| 투 포인터 알고리즘(Two Pointers Approach) (0) | 2022.02.15 |

