반응형
다익스트라 알고리즘은 그래프에서 최단 경로 문제를 해결할 수 있는 알고리즘 중 하나이다.
최단 경로 문제이므로 각 간선에는 가중치(거리)가 존재하며,
가중치가 음수인 간선이 존재한다면 다익스트라 알고리즘을 사용할 수 없다.
이해를 위해 아래의 예시를 살펴보자
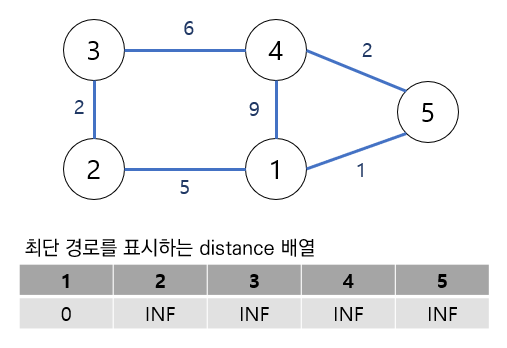
1번 노드부터 모든 경로의 최단거리를 구하려고 한다.
1번 노드에서 본인의 거리는 0이므로 0으로 업데이트한 뒤 나머지 노드까지의 거리는 무한대로 설정한다.
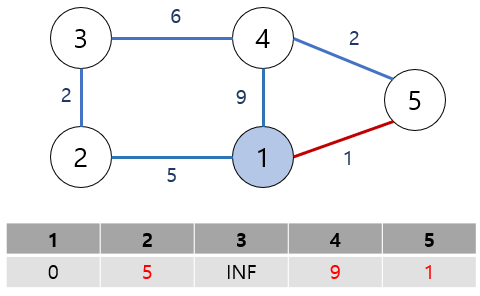
다음으로 1번과 연결된 노드들과의 거리를 업데이트해준다.
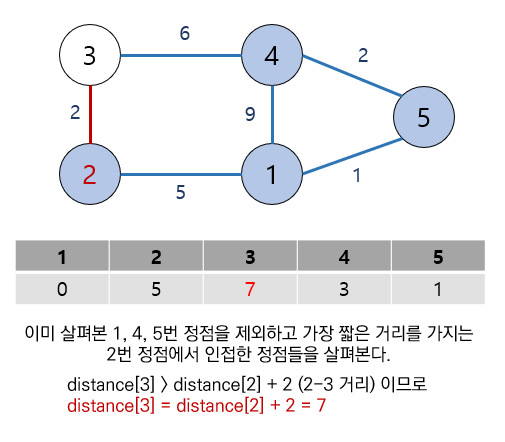
연결된 모든 노드들의 거리를 구했으면 가장 짧은 경로로 이동한다.
따라서 위의 예시에서는 5번 노드를 방문하여 다시 거리를 계산한다.
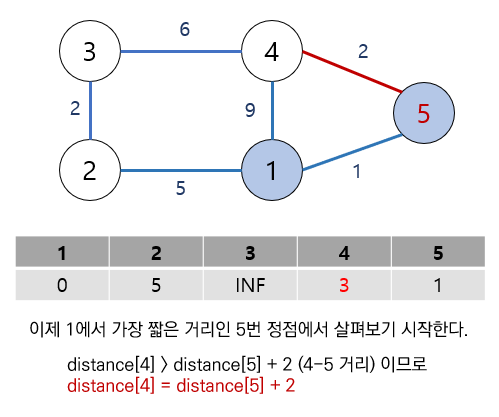
즉, 원래의 distance[4]는 9이지만 distance[5] = 1과 5에서 4로 이동하는 거리 2를 더하면
3으로 9보다 짧다. 따라서 distance[4]를 3으로 업데이트 시켜준다.
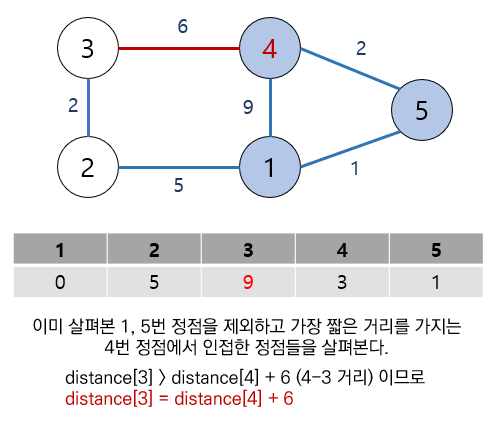
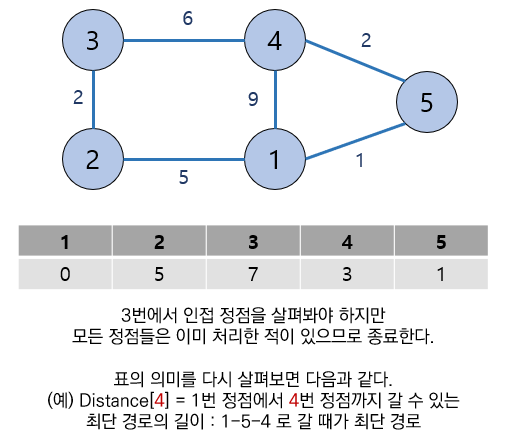
구현
우선순위 큐로 구현하는 방법과 배열로 구현하는 방법이 존재한다.
각각의 시간 복잡도는 노드의 개수가 V 간선의 개수가 E일 때
배열 : O(V^2), 우선순위 큐 : O(E logV)로 우선순위 큐로 구현하는 방법이 더 빠르다.
따라서, 우선순위 큐로 구현하는 방법만 알아본다.
int dist[MAX];
vector<pair<int, int> > graph[MAX];
void Dijkstra(){
priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > pq;
//최단 거리를 pop하기 위해 min heap으로 생성
//우선순위 큐를 사용하기 위해 first는 가중치, second는 노드
pq.push(make_pair(0, start));
dist[start] = 0;
while(!pq.empty()){
int curDist = pq.top().first;
int curNode = pq.top().second;
pq.pop();
if(dist[curNode] < curDist) continue;
for(int i=0; i<graph[curNode].size(); i++){
int nextNode = graph[curNode][i].first;
int nextDist = graph[curNode][i].second;
if(dist[nextNode] > curDist + nextDist){
dist[nextNode] = curDist + nextDist;
pq.push(make_pair(dist[nextNode], nextNode));
}
}
}
}코드에는 없지만, 모든 dist 배열은 INF로 초기화 시켜야한다.
반응형
'Programming Solve > 자료구조 & 알고리즘' 카테고리의 다른 글
| 이진 탐색(Binary Search) (0) | 2022.03.03 |
|---|---|
| 정렬의 종류 및 구현(C++) (0) | 2022.03.01 |
| 투 포인터 알고리즘(Two Pointers Approach) (0) | 2022.02.15 |
| 트리 구조 - 개념 및 예제 (0) | 2022.01.27 |

