반응형
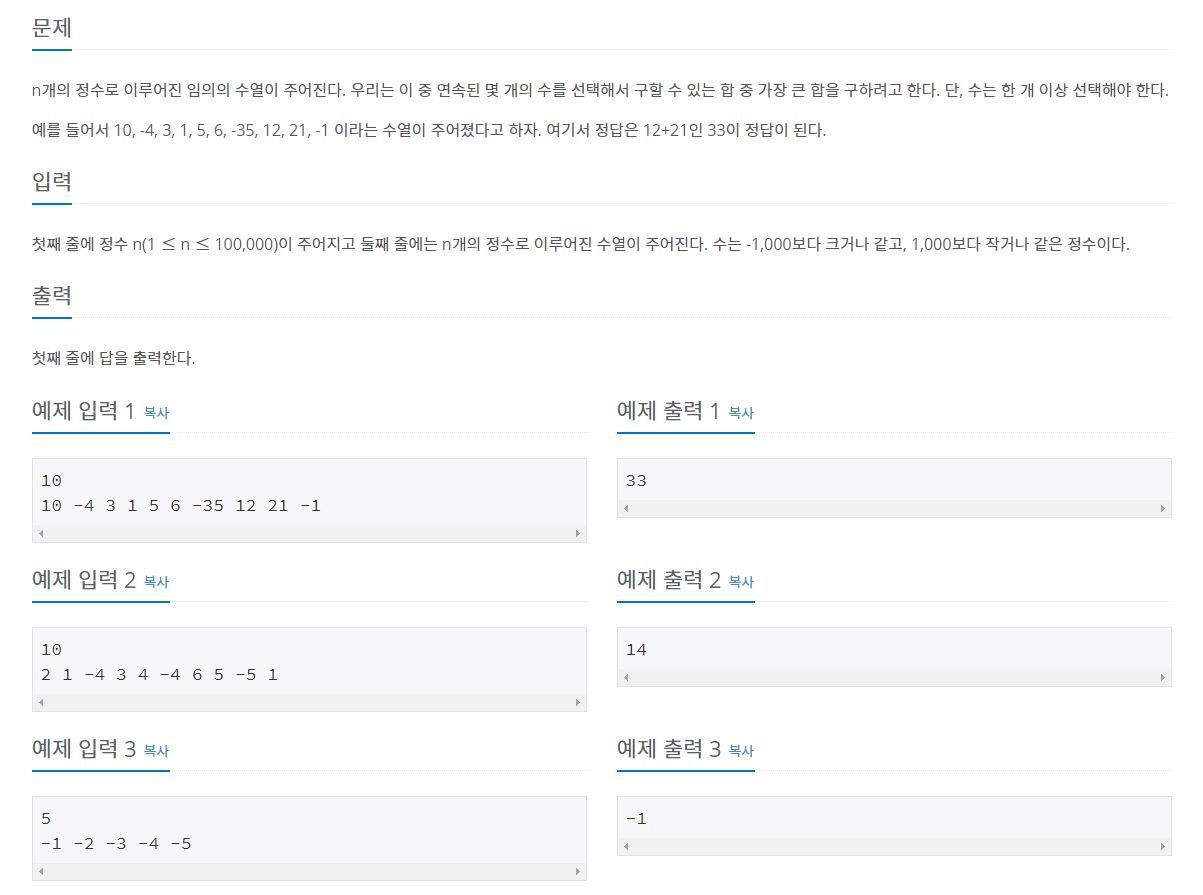
1. 문제
2. 아이디어
Dynamic Programming은 점화식만 세우면 80~90%는 풀었다고 할 수 있다.
연속된 몇 개의 수의 합 중 최댓값을 구하는 문제이므로 현재값과 누적된 값 + 현재값 중 어떤 것이 더 큰지
비교해보면 답을 구할 수 있을 것이다.
-> 만약 누적된 값에 현재값을 더한 것보다 그냥 현재값이 더 크다면 현재값부터 다시 더해나가는것이
더 큰 값이 될것이다 라는 아이디어이다.
점화식을 세우면 DP[i] = max(arr[i], DP[i-1] + arr[i]) 이고
예제 1의 케이스로 보면
arr [0] [1] [2] [3] [4] [5] [6] [7] [8] [9]
10 -4 3 1 5 6 -35 12 21 -1
DP [0] [1] [2] [3] [4] [5] [6] [7] [8] [9]
10 6 9 10 15 21 -14 12 33 32
와 같이 DP[8]에서 정답을 구할 수 있다.
3. 소스코드
#include <iostream>
#include <algorithm>
using namespace std;
long long arr[100001];
long long DP[100001];
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
int n;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> arr[i];
}
DP[0] = arr[0];
for (int i = 1; i < n; i++) {
DP[i] = max(arr[i], DP[i - 1] + arr[i]);
}
cout << *max_element(DP + 0, DP + n);
}
값을 입력받는 arr 배열과 연속된 합을 저장하는 DP 배열을 선언하고 값을 입력받는다.
*main문의 윗 두 줄은 C++의 입출력속도를 향상시키기 위한 것이다.
그 다음 DP[0]에 arr[0]값을 넣어두고 1부터 n까지 앞서 세운 점화식에 의해 DP 배열을 채워나간다.
마지막으로 DP 배열의 0번째 주소부터 n번째 주소까지의 최댓값을 출력한다.
반응형
'Programming Solve > BOJ' 카테고리의 다른 글
| BOJ 20953 / C++ (0) | 2021.03.02 |
|---|---|
| BOJ 11558 The game of death / C++ (0) | 2021.02.12 |
| BOJ 15312 이름 궁합 / C++ (0) | 2021.02.11 |
| BOJ 2445 / C++ (0) | 2021.02.07 |
| BOJ 1475 (C++) (0) | 2020.12.01 |
